Updates
Post updated 3/20:
- Table now contains 353 lenses (a big thank you to Anton Largiader for the raw data).
- Added 200+ new lenses from Sigma, Tokina, Zenit, Zeiss, and Tamron.
- Added the following newly released Canon lenses:
- EF 300 f/2.8L IS II USM
- EF 400 f/2.8L IS II USM
- EF-S 18-135 f/3.5-5.6 IS
- EF-S 15-85 f/3.5-5.6 IS USM
- TS-E 17mm f/4L
- TS-E 24mm f/3.5L II
- EF 100mm f/2.8L Macro IS USM
Post updated 3/7:
- Added disclaimer, added additional assumptions to conditions for handholdability testing section.
Disclaimer
After some discussion across various communities, it is obvious that people think I am trying to come up with some kind of panecea to finding out which lens is better than another from a handholdability perspective. That is not my goal. My goal is to create a theoretical framework for which we might begin to compare lenses to one another under very specific circumstances. Read the conditions below and keep these in mind when you look at the final results. I have added several marked in red to indicate some excellent points brought up in discussing this work.
Eventually, of course, I hope to improve this framework. Please do consider this a v.1 effort :).
Conditions for Handholdability Testing
I did some math tonight where I calculated the " maximal handholdability" of various lenses under certain conditions. The conditions, as such, are laid out below:
- Photos are being taken of static subjects.
- We follow the 1/focal length rule for "safe hand-holding" to ensure reasonably sharp shots.
- We do not differentiate between FF and 1.5x, or 1.6x sensor sizes when calculating safe handholding speeds.
- We DO factor IS into the equation – 2 stops of IS is equivalent to 2 aperture stops (because we are assuming static subjects).
- We always use the MINIMUM focal length of the lens as a benchmark.
- We always use the MAXIMUM aperture value of the lens as a benchmark.
- IS benefits are based on manufacturer's claims, are measured in whole f-stops, and are not necessarily tied to real-world results.
- [added 3/7] We do not take into account lens weight, balance, or weight distribution, which are very important when handholding a lens.
- [added 3/7] We do not factor in innate photographer skill / technique / body types, which are also key factors in handholding a lens.
- [added 3/7] We do not factor in real-world IS improvements which are not captured in direct manufacturer's claims. For example, any hybrid IS improvements in the new Canon V. II telephoto lenses are not taken into account here.
- [added 3/7] While t-stops would be a more effective measure for "actual amount of light hitting the sensor," we currently do not factor this into our equation.
- [added 3/7] We do not factor in variable lens aperture, which has an impact on overall handholdability, not maximal handholdability (which is what we care about).
- [added 3/7] IS is known to become more effective at longer focal lengths, we do not take this into account.
With these assumptions, the handholdability of a lens only varies with the following parameters:
- The minimum focal length of the lens.
- The maximum aperture of the lens.
- Any claimed image stabilization advantages.
We can also infer the following rules from these parameters:
- Longer focal lengths decrease handholdability (inverse relationship).
- IS increases handholdability (direct relationship).
- Wider apertures increase handholdability (direct relationship).
Picking a Measure for Handholdability
There are a couple scenarios to consider when measuring how much light a lens is usable in. The first is when comparing one lens to another, directly. The second is when comparing a set of lenses amongst themselves. These two scenarios may seem the exact same, but there is a key difference. When comparing 2 lenses directly, we need only to answer the following 2 questions: "what is the difference in their apertures" and "what is the difference between their focal lengths." When comparing a set of lenses, things become a bit more complicated, because we need a generic measure for a single lens's handholdability. So, let's first go about deriving a formula to compare one lens to another, and then we can go about the task of making a generic measure for handholdability.
Scenario 1: Comparing 2 Lenses Directly
Our first task is simple: relate aperture and focal length together into some arbitrary measurement of handholdability. For example, it makes logical sense that a 24 mm lens can be safely used in lower light than a 50 mm lens of the same max aperture. Why? Because you can handhold the 24mm lens in 1 stop lower light (1/25th of a second vs 1/50th of a second) than the 50mm lens simply because of the difference in focal length. It also makes logical sense that given two lenses of identical focal length, the lens with the wider max aperture is handholdable in lower light. Neither of these cases needs explaining by themselves; however, when they are related together is when things get interesting. Using the rules I have defined above, we realize that an 85mm f/1.2 lens is actually less handholdable than a 14mm f/2.8 lens. Why? Because the combination of smaller aperture and shorter focal length of the 14mm combined still add up to a lens useable in lower light. How so? Read on.
Step 0: Taking IS into Account (or, Calculating Relative Max Aperture)
Before we can discuss F/numbers and aperture, we need to take a quick aside on how we deal with lenses which have IS. We'll call this measure relative max aperture, and it will depend on if we have any IS improvements to take into account. For example, if a lens has an f/2.8 maximum aperture opening and offers 4 stops of IS improvement, the relative max aperture would be f/1 (from the progression 2.8, 2, 1.4, 1). The formula we use to calculate this is below:
- r = relative max aperture
- a = max aperture of the lens
- i = stops of is improvement
(1)
Whenever you are calculating the max aperture of a lens, be sure to take this into account (remember, only works for static subjects!) We will not use this formula until much later in our discussion.
Step 1: Find How F/Number Varies with Aperture Area
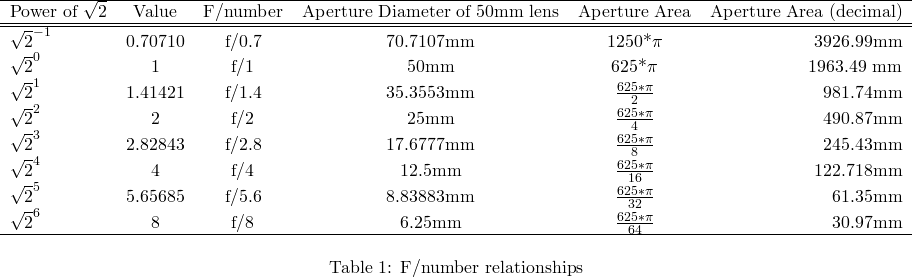
Ok, now that IS is out of the way, we first need to calculate the number of stops difference between the two lenses. We already know that aperture varies with the square root of 2. Why? Because each 1 stop increase in F/number represents a halving of the area of the aperture opening:
There is a pattern we can discover in the table above. Namely, every time the F/number increases exponentially with √2, the aperture area doubles. Because a doubling of the aperture area represents an increase of 1 stop of light hitting the sensor, we can codify this relationship as follows: "how many times must we double the area of the aperture opening of the slower lens to equal the area of the aperture opening of the faster lens?" The equation below expresses this relationship:
- afast = area of the aperture opening of the faster lens
- aslow = area of the aperture opening of the slower lens
- dav = number of doublings of aperture value
(2)
Step 2: Find How to Writing the Above Formula in Terms of F/Number
Now, while this formula is interesting, we want it in terms of F/number, not aperture opening area. If you remember, I mentioned above that every power of √2 increase of the F/number leads to a doubling of the aperture area. Because of this relationship, we can say simply replace the doubling factor in our above equation with the √2, to answer the question "how many times must we increase the F\number of a faster lens by √2 to equal the F\number of a slower lens?" E.g.:
- fslow = F/number of the slower lens
- ffast = F/number of the faster lens
- dav = number of doublings of aperture value
(3)
You may notice that we've swapped the location of the slow and fast lens in the below. This is because area varies inversely with the F/Number.
Step 3: Solve the Equation Above for the Number of Doublings (Stops)
Given this, we are ready to solve this equation for x, which will give us the number of stops of difference between two F/numbers.
First, divide both sides by fslow…
(4)
Now, take the log base √2 of both sides to remove the exponent…
(5)
Then convert to log base 10 by dividing the right sides by log(√2)…
(6)
If you know log rules, this should look familiar, because we can now simplify it to…
(7)
Step 4: Find Out a Method for Accounting for Focal Length
So, we see that the 85/1.2 is approximately 2.5 stops faster than the 14/2.8. Now, the only thing left to do now is to take into account the difference in focal lengths. To do so, we need to answer the question "how many times must we double the shorter focal length to equal the longer focal length." This question is derived from how shutter speeds work. As we already know, as you change aperture size, the shutter speed varies inversely with the square of the difference. The same applies to focal length when using the 1/focal length handholdability rule. For every doubling of the focal length, we effectively lose 1 stop of handholding power. So, in comparing a 24mm lens to a 50mm lens, we can deduce that the 24mm lens is approximately twice as handholdable. This relationship is expressed in the following equation:
- lshort= short focal length
- llong= long focal length
- dfl = number of doublings of focal length
(8)
Looks similar, right? It should, it's exactly the formula we derived above, but with a different doubling factor. This time, we know that to find the difference between two focal lengths, we just need to apply a straight factor of 2, not some root of 2 madness we had to deal with when concerning ourselves with the F/Number. We'll derive this formula in almost exactly the same way as we did the previous.
First, divide both sides by lshort
(9)
Now, take the log base 2 of both sides to remove the exponent…
(10)
Then convert to log base 10 by dividing both sides by log(2)…
(11)
If you know log rules, this should look familiar, because we can now simplify it to…
(12)
Step 5: Compare to our Previous Formula
Which is ALMOST exactly what we used to calculate the differences in stops of the lens aperture value.
(13)
What is the difference? Let's compare the two equations. As you can see, the only difference is what logarithm is on the bottom of the equations. Think of the value inside the bottom logarithm in the equations below as "the factor which represents a doubling of the value." For example, in the formula relating aperture openings, we know that the F\number is derived from powers of the square root of 2, as follows from our table above above. When we go from, say, F/1 to F/1.4, we also know that we lose a stop of handholdability, and that those values are related with the square root of 2. Similarly, in the formula relating focal length, we know that each time the focal length doubles, we lose a stop of handholdability, and that these values are related with a straight doubling factor of 2.
Step 6: Plug in Values and Evaluate
So, now we have a formula for finding the difference in f-stops of handholdability between two lenses given their apertures, and another formula for finding the difference in f-stops of handholdability between two lenses given their focal lengths. Let's compare the Canon 85/1.2 to the Canon 14/2.8 and see, once and for all, which is more handholdable. First, to find the difference in maximum aperture of the two lenses:
- fslow = 2.8
- ffast = 1.2
- dav= ?
(14)
(15)
(16)
So, the 85/1.2 is approximately 2.4 stops brighter than the 14/2.8. We still need to take into account the focal lengths, however, which is where things get interesting:
- lshort= 14
- llong= 85
- dfl = ?
(17)
(18)
(19)
Step 7: Analyze the Results
Now, when we look at the results of this last equation, we see the surprise (at least to me :)) Even though the 85/1.2 is 2.4 stops brighter than the 14/2.8, the 14/2.8 is still more handholdable because it's shorter focal length makes it useable at shutter speeds that are 2.6 stops slower than the 85/1.2! We can make this relationship generic such that we can have a single formula that can answer the question "given two lenses, which is more handholdable?" First, we assume that that the faster of the two lenses will always be more handholdable (with IS taken into account), therefore:
- The slower lens is more handholdable than the faster lens if and only if it has a sufficiently short focal length:
(20)
(21)
Step 8: Compare Lenses with our Formula
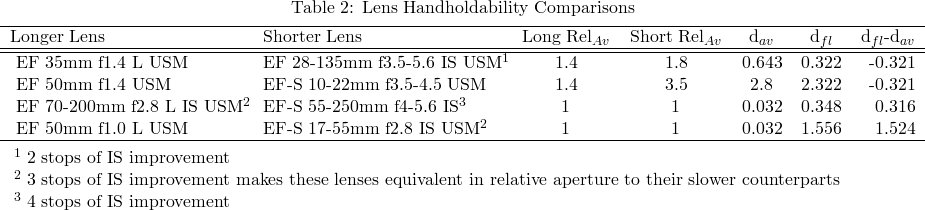
So, let's compare some Canon lenses and see how they stack up against one another:
Here is how you interpret this table:
- If the final column (dfl-dav) is negative, then you know that the longer lens is more handholdable.
- If the final column is positive, then you know that the shorter lens is more handholdable.
- If they are equal, then there is no difference in handholdability between these two lenses.
So, let's discuss each table row and what they mean in the real world:
- The 35/1.4 is 1/3rd of a stop more handholdable than the 28-135/3.5-5.6 IS, despite the 2 stop IS improvement of the latter.
- The 50/1.4 is 1/3rd of a stop more handholdable than the 10-22/3.5-4.5.
- The 70-200/2.8 I IS is 1/3rd of a stop less handholdable than the 55-200/4-5.6 IS.
- The 50/1.0 is 1.5 stops(!) less handholdable than the 17-55/2.8 IS.
Scenario 2: Comparing the Set of All Lenses
Now that we've found a formula to compare two lenses directly based on differences in their focal lengths and apertures, we can discuss how we might adapt this knowledge to create a general formula for comparing any number of lenses to one another. To do this, we must find a measurement that relates aperture and focal length to some direct measure of how dark a scene is. This is actually very straightforward, and the photographic community already has a way to measure it: Exposure Value. Exposure value is defined as "a measure which denotes all the combinations of a camera's shutter speed and aperture which give the same exposure at ISO 100," and will allow us to find a single number to represent how little light a lens can be safely handheld in. You can think of EV as relating directly to the amount of light present in a given scene. In fact, photographers already have another measure for the amount of light present in a scene. This measure is called "Light Value", or LV, and it is an ordinal value which is calculated in stops and is defined such that LV(0) = the light level that requires an exposure of 1 second at f/1 at ISO 100 (ie, very dark). Let's take a look at common light values, how they relate to EV, and then how EV is calculated.
Step 0: Understanding Light Value and How it Relates to Exposure Value
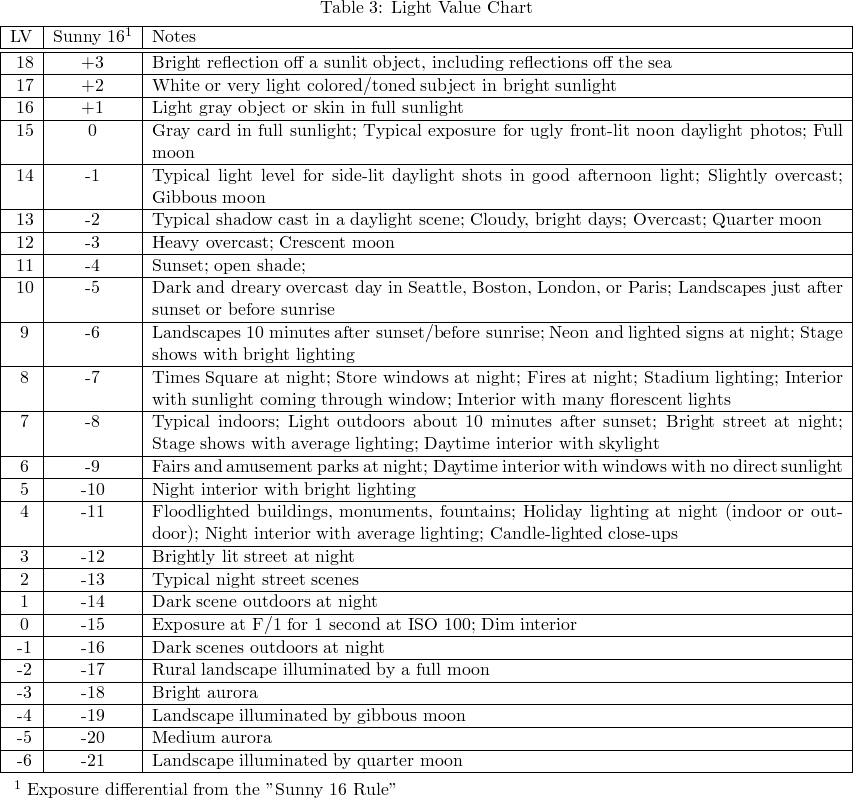
When we think about the handholdability of a particular lens, one interesting question we might ask is how dimly lit a scene we can shoot sharply with a given scene. As we discussed above, light value measures, effectively, how bright or dark a scene is. It does so by pegging a value of zero at a given brightness, and then letting all other values fall as they may. Each increase of 1 LV represents an increase of 1 stop. You can see an example of light values and how they map to particular scenes below (data taken from wikipedia, kenrockwell.com, and photokaboom.com).
So, how is light value related to exposure value? Quite simple:
EV = LV @ ISO 100
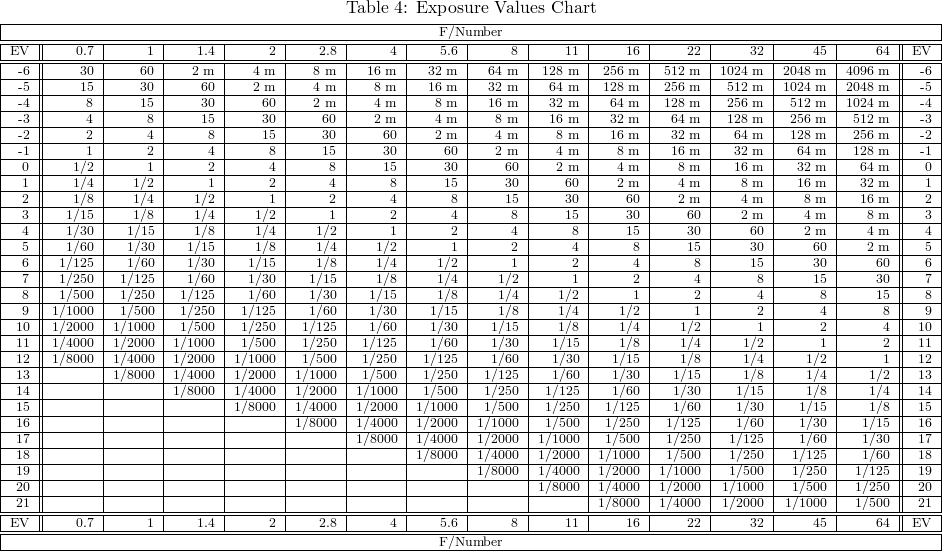
This means that, as long as we are at ISO 100, LV = EV. As soon as we increase ISO, however, we must change the equivalent EV to compensate for the difference. For example, if you are shooting a sunset and want to know what exposure to make at ISO 800, you would first look up the appropriate LV for that scene, which in this case is 8, and then compensate for the increased ISO by shifting the corresponding EV up by 3 stops (since ISO 800 is 3 stops more exposure than ISO 100). So, in this case, you would choose an exposure which is aligned with LV(11), and you would say that your sunset scene has an exposure value at ISO 800 of 11, or, in other terms: EV800 = 11. If you have an F/2.8 lens available to you, you can look at an EV chart and learn that the exposure you need is 1/250 @ F2.8. Below is a table of common exposure values so that you can see once and for all how LV, EV, and given camera settings are related.
Step 1: Examine How EV is Calculated
The formula for calculating EV is below:
- N = F/Number
- t = shutter speed
(22)
Remember, we need to get this formula in terms of F/Number (which it already is) and Focal Length (which it isn't). So how can we get focal length into the equation? Well, remember the golden rule of handholdability relates just that, focal length to shutter speed, e.g shutter speed at a minimum must be equal to 1/focal length.
Step 2: Refactor the EV Equation in Terms of Focal Length
- N = F/Number
- t = shutter speed = 1 / focal length = 1 / f
(23)
So what does this formula tell us? Simple: "the lowest exposure value at which a given lens at maximum aperture can be handheld." This may seem innocuous, but it allows us to assign a single numeric value to any lens which indicates its innate handholdability. This is obviously very powerful, because now, all we need is a list of lenses, and we can find some interesting data. Fortunately for us, a giant list of Canon lenses is only a click away (used from to Gallery1.co.uk).
Step 3: Plug in Values and Examine Results
Without further ado, here's a bunch of data! First, a chart which shows many of the current Canon lenses and their associated handholdability ratings. Second, a graph which relates this data visually. A couple of surprises from this data:
- The most handholdable lens is…the 15-85 3.5-5.6 IS USM! This is mainly due to its 4 stop IS and relatively wide maximum aperture. Take this with a grain of salt, as it's actually equivalent to a 28.8 mm lens on your favorite crop body (but who changes their 1/focal length rule when shooting crop anyway!).
- The EF 200/2 IS is quite high in handholdability. Mainly due to its MASSIVE aperture and 5 stop IS.
- Lots of commodity lenses are in the top 20: 15-85, 18-55, 18-200, 17-85, 55-250…just goes to show that you don't need to buy L if you are shooting still subjects in the dark!
- Surprisingly, the super fast primes are slightly lower in the list than expected – #10 for the 24/1.4, and #12 for the 50/1.0.
- The 70-200/2.8 IS version 1 is no slouch in 13th place. The newer version would beat out even some of the fast primes, since it gains a stop in IS improvement.
Conclusions and Next Steps
Well, if you've read this far, I applaud you. I've tried to make this post as readable as possible, and would really appreciate feedback in that regard. To summarize, we've learned:
- What to care about when discussing handholdability, namely max aperture, and focal length.
- How to relate focal length and max aperture together to compare one lens directly to another.
- What EV and LV are and why they matter for this discussion.
- How EV and LV can lead to us to a more generic solution for all lenses.
If you would like to download the spreadsheet which contains the data I've laid out in the chart and graph above, you can get it below. Please, if you use this data or information on your site, send a friendly pointer my way.
In the future, I hope to codify this data into an interactive tool that allows people to play with some variables that I have left out for this discussion. I hope you have found this useful, I know I have!
Happy shooting!
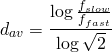








{ 1 trackback }